Multilevel Storage and Redundant Arithmetic
MathJax.Hub.Config({tex2jax: {inlineMath: [[‚$`‘,’`$‘], [‚\\(`‘,’`\\)‘]]}});
div.wp-caption img{padding: .5em;}
Besides the non-volatility memristors show another useful property, when it comes to its storage capability. Since the transitions between LRS and HRS are a gradual process, we can abort it inbetween. This way we can generate multiple stable states between LRS and HRS. Because of this memristors have multi-level cell (MLC) capability, i.e. they can store more than 2 values.
This allows not only to store data more densely, but to explore multi-valued logic and non-unique number representations, without an increase in number of bits needed to store results and intermediary results.
Our working group is researching ternary number representations and optimized arithmetic units based on this principle. Ternary numbers are represented using the digits \(`\{-1,0,1\}`\) instead of \(`\{0,1\}`\) as used in the usual binary encoding. Ternary numbers are not unique, for example can the 2-bit number 1, normally represented as 01, also represented using the ternary representations 01 and 1-1. It can easily be seen, that the equality of these numbers hold:
\(`1 = \mathtt{01} = 0 \times 2^1 + 1 \times 2^0 = 1 \times 2^1 + -1 \times 2^0 = \mathtt{1{-1}} = 1`\)
Using this representation it is possible to construct an adder that works in constant time and uses linear space with respect to the number of trits. This beats the conventional adders, the carry-ripple adder and the carry-lookahead adder.
Construction
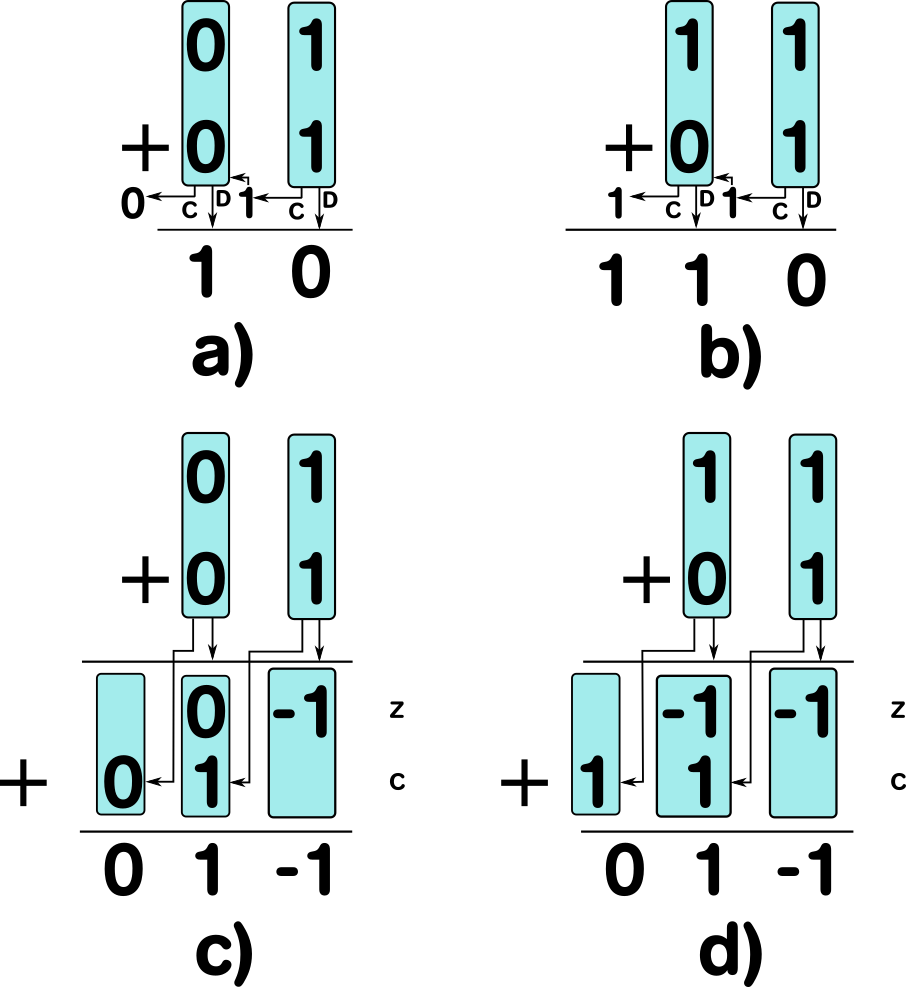
To understand how our adder works, one needs to understand what aspect actually makes addition problematic: First consider the addition of 01 + 01 (See Figure ? a)). In this example we first add the first place which yields a carry and add it to the sum of the second digits which is 0. In this case we could also have calculated the digits in parallel, since no additional carry was generated by an incoming carry of a digit to the right. But this is always a possibility: For example, consider 11 + 01 (See Figure ? b)). The addition of the first digit gives 0 and a carry. The sum of the second digits gives 1. In this case the carry of 1 + 1 of the right digit generates another carry to the right. It can be seen, that having 0 + 1 or 1 + 0 in a digit will give 1 and will trigger an outgoing carry, if there is an incoming carry. We therefore try to avoid having digits add up 1.
Our method is a two-step process. At first we generate a carry-vector c and a sub-total z of the digits and then add these up. The way we generate the carry-vector and the sub-total avoids digit-sum being 1. For the addition of 1 and 1 we get 0 for the sub-total and 1 for the carry. For 0 and 0 we get 0 for both the carry and the sub-total. So far, this is nothing noteworthy, since this is how a conventional full adder works. For the 0 + 1 and 1 + 0 cases we do not generate 0 as carry and 1 as sub-total, but instead 1 for the carry and -1 for the sub-total. Recall that \(`1 = \mathtt{01} = 0 * 2^1 + 1 * 2^0 = 1 * 2^1 + -1 * 2^0 = \mathtt{1{-1}} = 1`\). This first step can be performed independently for every digit and therefore has a time complexity of \(`\mathcal{O}(1)`\) and a space complexity of \(`\mathcal{O}(n)`\). You can see examples in Figure ? c) and d).
In the next step we add the carry and the sub-total. The sub-total can only contain -1 and 0 as digits and the carry-vector only 0 and 1, because of the rules stated in the previous paragraph. The addition of carry and sub-total can not generate carries at all and can be done with half adders alone and therefore has a time complexity of \(`\mathcal{O}(1)`\) and a space complexity of \(`\mathcal{O}(n)`\). Since the signals of the sub-total and the carry-vector each only use two values this process can be implemented in regular CMOS, without needing multi-valued logic. Only the storage of the operands needs three-level cells for the trits (ternary digits).
Since the time and space complexities of the two steps are equal, we get for the whole process a time complexity of \(`\mathcal{O}(1)`\) and a space complexity of \(`\mathcal{O}(n)`\) for n-digit adders.
Comparison to Carry-Ripple Adder
The carry-ripple adder is built from 1-bit full adders. It uses space proportional to the bit width, as it doesn’t use any additional hardware to theses adders. Our ternary adder also scale linearly with the number of trits.
But the carry-ripple adder has a runtime complexity of \(`O(n)`\), since each full adder has to wait for the carry of the previous full adder, except the first one. Our adder can provide the result in \(`O(1)`\), since its digits can work independently.
Comparison to Carry-Lookahead Adder
The carry-lookahead adder tries to alleviate the “rippling” of the carry bits, by adding a “lookahead unit” that predicts weather a carry is possible for a block of bits or not. This unit has a space complexity of \(`O(n \log n)`\) and reduces the delay complexity down to \(`O(\log n)`\).
For more information see our papers on this topic:
D. Fey, “Using the multi-bit feature of memristors for register files in signed-digit arithmetic units,” Semiconductor Science and Technology, vol. 29, no. 10, p. 104008, Oct. 2014. D. Fey, M. Reichenbach, C. Söll, M. Biglari, J. Röber, and R. Weigel, “Using Memristor Technology for Multi-value Registers in Signed-digit Arithmetic Circuits,” 2016, pp. 442–454. D. Fey, “Evaluating Ternary Adders using a hybrid Memristor / CMOS approach,” arXiv:1701.00065 [cs], Dec. 2016.
